MANAGEMENT: EXAM PREPARATIONS BANK,MAT,CAT FREE MATERIAL

Quadrilateral

A quadrilateral is a polygon with four sides (edges) and four vertices (corners). The word quadrilateral is made of the words quad (meaning four) and lateral (meaning sides). So, quadrilateral is simply a four sided figure.

The sum of interior angles for all quadrilaterals must be equal to 360 degrees.

Types of Quadrilaterals

Square
Rectangle
Parallelogram
Rhombus
Trapezoid

Quadrilateral: Square & Rectangle

Square: A square has four equal sides and four equal angles (90-degree angles or right angles).

Perimeter of Square

Perimeter of the square is 4 times the length of the side. For a square of length L, perimeter = 4 * L

Area of Square

Area of square is the square of length of the side. Area = L * L

Properties of Square

The diagonals of a square bisect each other and meet at right angles (90 degrees)
The diagonals of a square bisect its angles
The diagonals of a square are perpendicular
Opposite sides of a square are both parallel and equal in length
All four angles of a square are equal. (every angle of a square is a right angle)
The diagonals of a square are equal.

Rectangle: A rectangle is a quadrilateral with 4 right angles. It is similar to square except that its sides are not equal.

Perimeter of Rectangle

Perimeter of the rectangle is sum of the length of its sides. Perimeter = 2 * (Length + Breadth)

Area of Rectangle

Area of rectangle is multiplication of its length and breadth. Area = Length * Breadth

Properties of Rectangle

All angles are right angles (90 degrees)
Opposite sides are parallel and equal.
Diagonals bisect each other.
Quadrilateral: Parallelogram

A parallelogram is a quadrilateral with two pairs of parallel sides.

Properties of parallelogram

Each diagonal divides the quadrilateral into two congruent triangles with the same orientation.
The opposite sides are parallel and equal in length.
The diagonals bisect each other.
The opposite angles are equal in measure.
The sum of the squares of the sides equals the sum of the squares of the diagonals. (Parallelogram Law)
Adjacent angles are supplementary (180 degrees).
Square, Rectangle and Rhobus are special types of parallelograms.

Perimeter & Area of parallelogram

The perimeter of parallelogram is sum of the length of its sides. Perimeter = 2(L + B)

Area of parallelogram is multiplication of its longer side and distance between them. Area = L * H

Parallelogram Law

It states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals. If ABCD is parallelogram, then

In case of rectangle and square, this law reduces to pythagoras theorem.

Mensuration

Mensuration is the branch of mathematics which deals with the study of geometric shapes, their area, volume and different parameters in geometric objects.

Important Mensuration Formulae

1. Area of rectangle (A) = length(l) * Breath(b) 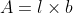$A = l \times b$

2. Perimeter of a rectangle (P) = 2 * (Length(l) + Breath(b)) 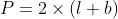$P = 2 \times(l + b)$

3. Area of a square (A) = Length (l) * Length (l) A = 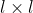$l \times l$

4. Perimeter of a square (P) = 4 * Length (l) 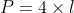$P = 4 \times l$

5. Area of a parallelogram(A) = Length(l) * Height(h) 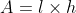$A = l \times h$

6. Perimeter of a parallelogram (P) = 2 * (length(l) + Breadth(b)) 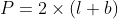$P = 2 \times (l + b)$

7. Area of a triangle (A) = (Base(b) * Height(b)) / 2 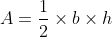$A = \frac{1}{2} \times b \times h$

Perimeter = (a + b + c)

Area of triangle = $A = \sqrt{s(s-a)(s-b)(s-c)}$ [Hero’s formula]

8. Area of triangle (A) = 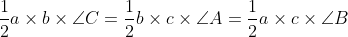$\frac{1}{2} a \times b \times \angle C = \frac{1}{2} b \times c \times \angle A = \frac{1}{2} a \times c \times \angle B$

9. Area of isosceles triangle = 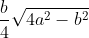$\frac{b}{4}\sqrt{4a^2 - b^2}$

10. Area of trapezium (A) = 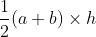$\frac{1}{2} (a+b) \times h$

11. Perimeter of a trapezium (P) = sum of all sides

12. Area of rhombus (A) = Product of diagonals / 2

13. Perimeter of a rhombus (P) = 4 * length

14. Area of quadrilateral (A) = 1/2 * Diagonal * (Sum of offsets)

15. Area of a Kite (A) = 1/2 * product of it’s diagonals

16. Perimeter of a Kite (A) = 2 * Sum on non-adjacent sides

17. Area of a Circle (A) = 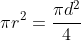$\pi r^2 = \frac{\pi d^2}{4}$

18. Circumference of a Circle = 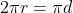$2 \pi r = \pi d$

19. Total surface area of cuboid = 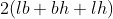2 (lb + bh + lh)

20. Total surface area of cuboid = 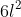6 l^2

21. length of diagonal of cuboid = 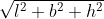$\sqrt{l^2+b^2+h^2}$

22. length of diagonal of cube = 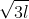$\sqrt{3 l}$

23. Volume of cuboid = l * b * h

24. Volume of cube = l * l * l

25. Area of base of a cone = 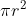$\pi r^2$

26. Curved surface area of a cone = C = {tex inline}\pi r l{tex}

27. Total surface area of a cone = 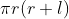$\pi r (r+l)$

28. Volume of right circular cone = 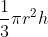$\frac{1}{3} \pi r^2 h$

29. Surface area of triangular prism = (P * height) + (2 * area of triangle)

30. Surface area of polygonal prism = (Perimeter of base * height ) + (Polygonal base area * 2)

31. Lateral surface area of prism = Perimeter of base * height

32. Volume of Triangular prism = Area of the triangular base * height

33. Curved surface area of a cylinder = 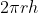$2 \pi r h$

34. Total surface area of a cylinder = 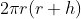$2 \pi r(r + h)$

35. Volume of a cylinder = 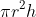$\pi r^2 h$

36. Surface area of sphere = 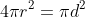$4 \pi r^2 = \pi d^2$

37. Volume of a sphere = 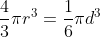$\frac{4}{3} \pi r^3 = \frac{1}{6} \pi d^3$

38. Volume of hollow cylinder = 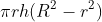$\pi r h(R^2-r^2)$

39. Surface area of a right square pyramid = 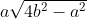$a \sqrt{4b^2 - a^2}$

40. Volume of a right square pyramid = 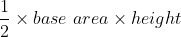$\frac{1}{2} \times base \, \, area \times height$

41. Area of a regular hexagon = 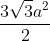$\frac{3\sqrt{3}a^2}{2}$

42. area of equilateral triangle = 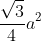$\frac{\sqrt{3}}{4} a^2$

43. Curved surface area of a Frustums = 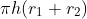$\pi h (r_1 + r_2)$

44. Total surface area of a Frustums = 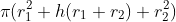$\pi (r_1^2 + h(r_1+r_2) + r_2^2)$

45. Curved surface area of a Hemisphere = 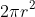$2 \pi r^2$

46. Total surface area of a Hemisphere = 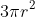$3 \pi r^2$

47. Volume of a Hemisphere = 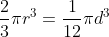$\frac{2}{3} \pi r^3 = \frac{1}{12} \pi d^3$

48. Area of sector of a circle = 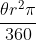$\frac{\theta r^2 \pi}{360}$

Vedic Maths - Introduction

Vedic Mathematics is a system of mathematics consisting of a list of 16 basic sutras, or aphorisms. They were presented by a Hindu scholar and mathematician, Bharati Krishna Tirthaji Maharaja, during the early part of the 20th century.

The calculation strategies provided by Vedic mathematics are said to be creative and useful, and can be applied in a number of ways to calculation methods in arithmetic and algebra.

16 Sutras translated in English (from Sanskrit) are:

By one more than the one before
All from 9 and the last from 10
Vertically and Cross-wise
Transpose and Apply
If the Samuccaya is the Same it is Zero
If One is in Ratio the Other is Zero
By Addition and by Subtraction
By the Completion or Non-Completion
Differential Calculus
By the Deficiency
Specific and General
The Remainders by the Last Digit
The Ultimate and Twice the Penultimate
By One Less than the One Before
The Product of the Sums
All the Multipliers

It is amazing that with the help of Vedic Mathematics, you will be able to solve or calculate complex mathematical problems mentally.

By one more than the previous one

1. Square of numbers ending in 5

65 x 65 = (6 x (6+1) ) 25 = (6x7) 25 = 4225

45 x 45 = (4 x (4+1) ) 25 = (4x5) 25 = 2025

105 x 105 = (10 x (10+1) 25 = (10 x 11) 25 = 11025

2. When sum of the last digits is the base(10) and previous parts are the same

44 x 46 = (4 x (4+1)) (4 x 6) = (4 x 5) (4 x 6) = 2024

37 x 33 = (3 x (3+1)) (7 x 3) = (3 x 4) (7 x 3) = 1221

11 x 19 = (1 x (1+1)) (1 x 9) = (1 x 2) (1 x 9) = 209

MANAGEMENT

Monday, June 4, 2012

EXAM PREPARATIONS BANK,MAT,CAT FREE MATERIAL