MANAGEMENT: EXAM PREPARATIONS BANK,MAT,CAT FREE MATERIAL

Progressions

A Progression is a sequence of numbers which have some kinf of relation. This relation determines what kind of a progression is. Generally, there are two types of progressions:

Arithmetic Progression (AP)
Geometric Progression (GP)

Any progression (AP or GP) can be generally expressed as

$a_1 + a_2 + a_3 +\dots+ a_{n-1} + a_n$

Total Terms:

First Term: 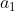a_1

Last Term: 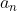a_n

Arithmetic Progression

In AP, the relation amoung sequence of numbers is that the difference between any two successive numbers is same.

Example: 3, 5, 7, 9, 11, 13, ... is an AP with difference 2. This difference is called common difference.

$S_n=\frac{n}{2}( a_1 + a_n)=\frac{n}{2}[ 2a_1 + (n-1)d]$

Geometric Progression

In GP, each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio.

Example: 2, 6, 18, 54, ...

$a + ar + ar^2 + ar^3 + ar^4 + \cdots$

$a_n = a\,r^{n-1}$

Functions

A function is a rule which indicates an operation to perform.

Graph Transformations

y = f(x) + a is the same as the graph y = f(x), shifted upwards by a units.
y = f(x - a) shifts the graph a units to the right.
y = f(ax) is a stretch with scale factor 1/a parallel to the x-axis.
y = a.f(x) is a stretch with scale factor a parallel to the y-axis.

Binomial Theorem

Binomial Expression: An algebraic expression consisting of two terms with a positive or negative sign between them. Example: (x+y)

The expansion of binomial expression raised to power n is called Binomial Theorem.

${(x + y)^n = x^n + ^nC_1x^{n-1}y + ^nC_2x^{n-2}y^2 + \dots + y^n}$

$^nC_1, ^nC_2, \dots , ^nC_n$ are Binomial Coefficients.

Points to Note:

There are total of (n+1) terms in the expansion.
In each term, sum of the indices of x and y is equal to n.

Indices and Surds

Laws of Indices

$a^m \times a^n = a^{m+n}$

$a^m \div a^n = a^{m-n}$

$(a^m)^n = a^{mn}$

$a^{1 \over m} = \sqrt[m]{a}$

$a^{-m} = \frac{1}{a^m}$

$a^{\frac{m}{n}} = \sqrt[n]a^m$

Logarithms

Logarithmic Identities

$\log_b(xy) = \log_b(x) + \log_b(y)$
$\log_b\!\left(\begin{matrix}\frac{x}{y}\end{matrix}\right) = \log_b(x) - \log_b(y)$
$\log_b(x^d) = d \log_b(x)$
$\log_b\!\left(\!\sqrt[y]{x}\right) = \begin{matrix}\frac{\log_b(x)}{y}\end{matrix}$
$x^{\log_b(y)} = y^{\log_b(x)}$
$c\log_b(x)+d\log_b(y) = \log_b(x^c y^d)$
$\log_b(1) = 0$

$\log_b(b) = 1$
$b^{\log_b(x)} = x$
$\log_b(b^x) = x$
$\log_a b = {\log_c b \over \log_c a}$

Permutation & Combination

Combination & Permutation deals with arrangement of thing. If the order doesn't matter, then it is called Combination. If the order does matter, then it is a Permutation.

In other words, Permutation is an ordered Combination.

Permutation

${^nP_r} = {n! \over {(n-r)!}$

There are basically two types of permutation:

When repetition is allowed
No repetition

1. Permutations with Repetition

To choose r things from n when repetition is allowed, the permutations are:

n × n × ... (r times) = n^r

(Because there are n possibilities for the first choice, then there are n possibilites for the second choice, and so on.)

Combinations

Number of ways objects can be selected from a group.

${^nC_r} = {{^nP_r} \over r!}$

Probability

Probability is the likelihood or chance of an event occurring.

Some Concepts

When we toss a coin, then either a Head (H) or a Tail (T) appears.
A dice is a solid cube ,having 6 faces,marked 1, 2, 3, 4, 5, 6 respectively. When we throw a die, the outcome is the number that appears on its upper face.
A pack of cards has 52 cards. It has 13 cards of each suit, namely spades, clubs, hearts and diamonds. Cards of spades and clubs are balck cards. Cards of hearts and diamonds are red cards. There are four honours of each suit. These are Aces, Kings, Queens and Jacks. These are called Face cards.

The probability of a certain event occurring can be represented by P(A). The probability of a different event occurring can be written as P(B). Therefore, for two events A and B,

$\displaystyle P(A) + P(B) - P(A\cap B) = P(A\cup B)$

Mutually Exclusive Events

Events A and B are mutually exclusive if they have no events in common. If two events are mutually exclusive,

$\displaystyle P(A) + P(B) = P(A\cup B)$

Independent Events

Two events are independent if (and only if)

$\displaystyle P(A\cap B) = P(A)P(B)$

Conditional Probability

Conditional probability is the probability of an event occurring, given that another event has occurred.

$\displaystyle P(A|B)$ means the probability of A occurring, given that B has occurred.

For two events A and B,

$\displaystyle P(A\cap B) = P(A|B)P(B)$

$\displaystyle P(A\cap B) = P(B|A)P(A)$

Triangles

Sum of the angles of a triangle is 180 degrees.

The sum of any two sides of a triangle is greater than third side.

Pythagoras Theorem: In a right angled triangle (Hypotenuse)² = (Base)² + (Height)²

The line joining the mid point of a side of a triangle to the opposite vertex is called the Median.

The point where the three medians of a triangle meet, is called Centroid. The centroid divides each of the medians in the ratio 2:1.

In an isosceles triangle, the altitude from the vertex bisects the base.

The median of a triangle divides it into two triangles of the same area.

The area of the triangle formed by joining the mid points of the sides of a given triangle is one-fourth of the area of the given triangle.

Similar Triangles

If the angles of one triangle are equal to the angles of another triangle, then the triangles are said to beEquiangular. Equiangular triangles have the same shape but may have different sizes. Therefore, equiangular triangles are also called Similar Triangles.

Two triangles are similar if their corresponding angles are equal and corresponding sides are proportional.

${AB \over DE} = {BC \over EF} = {CA \over FD}$

$\angle A = \angle D$

$\angle B = \angle E$

$\angle C = \angle F$

Properties

The ratio of area of similar triangles is equal to the square of ratio of sides.
If the ratio of corresponding sides equals to 1, then triangles become congruent.

MANAGEMENT

Monday, June 4, 2012

EXAM PREPARATIONS BANK,MAT,CAT FREE MATERIAL